圆周率100位
π=3.
圆周率1000位
π=3.
圆周率位数
圆周率π(Ratio of circumference to diameter;Pi)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比。是精确计算圆周长、圆面积、球体积等几何形状的关键值。在分析学里,π可以严格地定义为满足 sin(x)=0 的最小正实数x。
圆周率用字母π(读作pài)表示,是一个常数(约等于 3.141592654),是代表圆周长和直径的比值。它是一个无理数,即无限不循环小数。在日常生活中,通常都用3.14代表圆周率去进行近似计算。而用十位小数 3.141592654 便足以应付一般计算。即使是工程师或物理学家要进行较精密的计算,充其量也只需取值至小数点后几百个位。
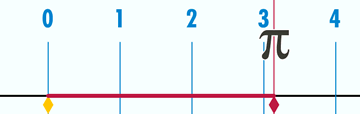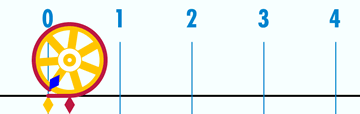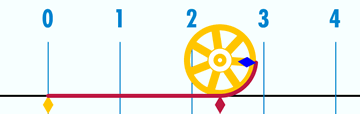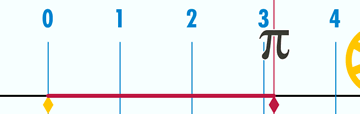
圆周率的记忆方法
世界纪录是100,000位,日本人原口证于2006年10月3日背诵圆周率π至小数点后100,000位。 普通话用谐音记忆圆周率的有“山巅一寺一壶酒,尔乐苦煞吾,把酒吃,酒杀尔,杀不死,乐而乐”,就是3.1415926535897932384626。另一谐音为:“山巅一石一壶酒,二妞舞扇舞,把酒沏酒扇又扇,饱死啰”,就是3.14159265358979323846。 英文中,会使用英文字母的长度作为数字来记忆圆周率,例如“How I want a drink, alcoholic of course, after the heavy lectures involving quantum mechanics. All of the geometry, Herr Planck, is fairly hard, and if the lectures were boring or tiring, then any odd thinking was on quartic equations again.”,就是 3.1415926535897932384626433832795。
圆周率是怎样算出来的
关于π最早的文字记载来自公元前2000年前后的古巴比伦人,它们认为π=3.125,而古埃及人使用π=3.1605。中国古籍里记载有“圆径一而周三”,即π=3,这也是《圣经》旧约中所记载的π值。在古印度耆那教的经典中,可以找到π≈3.1622的说法。这些早期的π值大体都是通过测量圆周长,再测量圆的直径,相除得到的估计值。
公元前3世纪,古希腊大数学家阿基米德第一个给出了计算圆周率π的科学方法:圆内接(或外切)正多边形的周长是可以精确计算的,而随着正多边形边数的增加,会越来越接近圆,那么多边形的周长也会越来越接近圆周长。阿基米德用圆的内接和外切正多边形的周长给出圆周率的下界和上界,正多边形的边数越多,计算出π值的精度越高。阿基米德从正六边形出发,逐次加倍正多边形的边数,利用勾股定理(西方称为毕达哥拉斯定理),就可求得边数加倍后的正多边形的边长。因此,随着边数的不断加倍,阿基米德的方法原则上可以算出任意精度的π值。他本人计算到正96边形,得出223/71<π<22/7,即π值在3.140 845与3.142 857之间。在西方,后人一直使用阿基米德的方法计算圆周率,差不多使用了19个世纪。
中国三国时期的数学家刘徽,在对《九章算术》作注时,在公元264年给出了类似的算法,并称其为割圆术。刘徽通过用圆内接正多边形的面积来逐步逼近圆面积来计算圆周率的。约公元480年,南北朝时期的大科学家祖冲之就用割圆术算出了3.141 592 6<π<3.141 592 7,这个π值已经准确到7位小数,创造了圆周率计算的世界纪录。
德国的鲁道夫·范·科伊伦花费大半生时间,计算了正262边形的周长,于1610年将π值计算到小数点后35位。德国人因此将圆周率称为“鲁道夫数”。
关于π值的研究,革命性的变革出现在17世纪发明微积分时,微积分和幂级数展开的结合导致了用无穷级数来计算π值的分析方法,1706年,英国数学家梅钦得出了现今以其名字命名的公式,给出了π值的第一个快速算法。梅钦因此把π值计算到了小数点后100位。1874年,英国的谢克斯花15年时间将π计算到了小数点后707位,这是人工计算π值的最高纪录,被记录在巴黎发现宫的π大厅。可惜后来发现其结果从528位开始出错了。
电子计算机出现后,人们开始利用它来计算圆周率π的数值,从此,π的数值长度以惊人的速度扩展着:1949年算至小数点后2037位,1973年算至100万位,1983年算至1000万位,1987年算至1亿位,2002年算至1万亿位,至2011年,已算至小数点后10万亿位。